One of the nice things about building sortvis.org and writing the posts that led up to it is that people email me with pointers to esoteric algorithms I've never heard of. Today's post is dedicated to one of these - a curious little sorting algorithm called cyclesort. It was described in 1990 in a 3-page paper by B.K. Haddon, and has become a firm favourite of mine.
Cyclesort has some nice properties - for certain restricted types of data it can do a stable, in-place sort in linear time, while guaranteeing that each element will be moved at most once. But what I really like about this algorithm is how naturally it arises from a simple theorem on symmetric groups. Bear with me while I work up to the algorithm through a couple of basic concepts.
Cycles
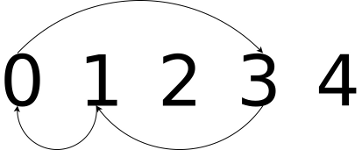
Lets start with the definition of a cycle. A cycle is a subset of elements from a permutation that have been rotated from their original position. So, say we have an ordered set [0, 1, 2, 3, 4], and a cycle [0, 3, 1]. The cycle defines a rotation where element 0 moves to position 3, 3 to 1 and 1 to 0. Visually, it looks like this:
We can apply a cycle to an ordered set to obtain a permutation, and we can then reverse that cycle to re-obtain the original set. Here's a Python function that applies a cycle to a list in-place:
def apply_cycle(lst, c):
# Extract the cycle's values
vals = [lst[i] for i in c]
# Rotate them circularly by one position
vals = [vals[-1]] + vals[:-1]
# Re-insert them into the list
for i, offset in enumerate(c):
lst[offset] = vals[i]
Here's an interactive session showing the function in action:
>>> lst = [0, 1, 2, 3, 4]
>>> c = [0, 3, 1]
>>> apply_cycle(lst, c)
>>> lst
[1, 3, 2, 0, 4]
>> c.reverse()
>> apply_cycle(lst, c)
>> lst
[0, 1, 2, 3, 4]
Permutations
Now, it's a fascinating fact that any permutation can be decomposed into a unique set of disjoint cycles. We can think of this as analogous to the factorization of a number - every permutation is the product a unique set of component cycles in the same way every number is the product of a unique set of prime factors. Taking this as a given, how could we calculate the cycles that make up a permutation? One obvious way to proceed is to pick a starting point, and simply "follow" the cycle in reverse until we get back to where we started. We know from the result above that the element is guaranteed to be part of a cycle, so we must eventually reach our starting point again. When we do, hey presto, we have a complete cycle. If we keep track of the elements that are already part of a known cycle, we can skip to the next unknown element and repeat the process. Once we reach the end of the list we're done.
This scheme can only work if we know where in the ordered sequence any given element belongs, because this is the way we find the "previous hop" in a cycle. In the examples above, we worked with lists that consist of a contiguous range of numbers 0..n, which gives us a short-cut: the element's value is its offset in the ordered list. In the code below I've factored this out into a function key, which takes an element value, and returns its correct offset - in this case key is simply the identity function.
Here's a Python function that finds all cycles in permutations of numbers ranging from 0..n:
def key(element):
return element
def find_cycles(l):
seen = set()
cycles = []
for i in range(len(l)):
if i != key(l[i]) and not i in seen:
cycle = []
n = i
while 1:
cycle.append(n)
n = key(l[n])
if n == i:
break
seen = seen.union(set(cycle))
cycles.append(list(reversed(cycle)))
return cycles
Running it on our example permutation produces the cycle we used to produce it:
>>> find_cycles([1, 3, 2, 0, 4])
>>> [[3, 1, 0]]
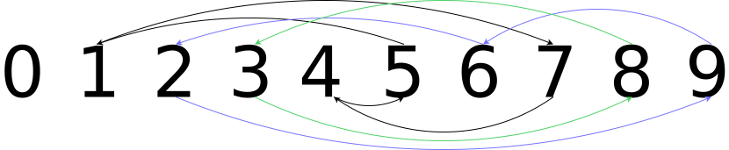
Here's find_cycles run on a longer, randomly shuffled list:
l = [0, 5, 6, 8, 7, 4, 9, 1, 3, 2]
>>> find_cycles(l)
>>> [[7, 4, 5, 1], [9, 6, 2], [8, 3]]
And here's a handsomely colourful graphical version of the output above:
A sorting algorithm emerges
Let's take a closer look at the find_cycles function above. We keep track of elements that are already part of a cycle in the seen set, so that we can skip them as we proceed through the list. The seen set can be as large as the list itself, so we've doubled the memory requirement for the algorithm. If we're allowed to destroy the input list, we can avoid explicitly tracking seen elements by relocating elements to their correct position as we work our way around each cycle. All the cycles are disjoint and we traverse each cycle only once, so doing this won't affect the function's output. We can then tell that we need to skip an element we've already seen by checking whether it's in the correct sorted position. Here's the result:
def key(element):
return element
def find_cycles2(l):
cycles = []
for i in range(len(l)):
if i != key(l[i]):
cycle = []
n = i
while 1:
cycle.append(n)
tmp = l[n]
if n != i:
l[n] = last_value
last_value = tmp
n = key(last_value)
if n == i:
l[n] = last_value
break
cycles.append(list(reversed(cycle)))
return cycles
But... at the end of this process, the original list is sorted! Tada: cyclesort pops out of the shrubbery almost as a side-effect of efficiently finding all cycles. If we're only interested in sorting, we can strip the code that saves the cycles, which leaves us with a nice, pared-back sorting algorithm:
def key(element):
return element
def cyclesort_simple(l):
for i in range(len(l)):
if i != key(l[i]):
n = i
while 1:
tmp = l[n]
if n != i:
l[n] = last_value
last_value = tmp
n = key(last_value)
if n == i:
l[n] = last_value
break
The cyclesort_simple algorithm only works on permutations of sets of numbers ranging from 0 to n. There are other fast ways to sort data of this restricted kind, but all the methods I know of require additional memory proportional to n. Cyclesort can do it without any extra storage at all, which is a neat trick.
Visualising cyclesort
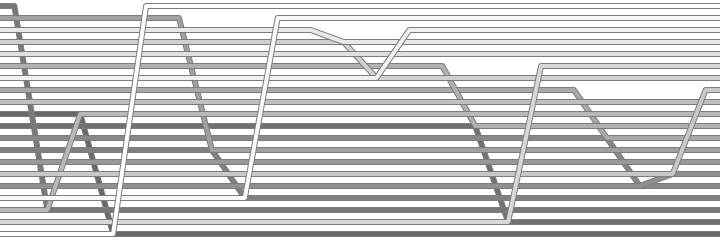
At this point, we have enough information to visualise the algorithm, so let's take a look at the beastie we're working with. I've had to make some little adjustments to the usual sortvis.org visualisation process to cope with cyclesort. In the algorithm above, the first element is duplicated into the second position of each cycle, and that duplicate remains in play until it's over-written by the last element of the cycle. I changed the algorithm slightly to write a null placeholder at the start of the cycle to avoid duplicates, and taught the sortvis.org visualiser to deal with "empty" slots. The resulting weave visualisation looks like this:
This is quite satisfying - you can tell where each cycle begins and ends by the gaps, which span each cycle exactly. It's immediately clear that the permutation above, for instance, contained five cycles. Within each cycle, you can follow along as each element replaces the next, until we finally close the gap by placing the last element in the first slot.
The dense visualisation is less informative because the gaps are too small to see at a single-pixel width, and the algorithm doesn't have much other large-scale structure. It still looks neat, though:
Generalising cyclesort
Cyclesort works whenever we can write an implementation of the key function, so there's quite a bit of scope for clever exploitation of structured data. The Haddon paper presents a solution for one common case: permutations whose elements come from a relatively small set, where the number of occurances of each element is known. The insight is that the key function can have persistent state, letting us calculate the positions of elements incrementally as we work through the list.
We begin by adding an extra argument to our sort function: a list (element, count) tuples telling us a) the order of the keys, and b) the frequency with which each key occurs.
[("a", 10), ("b", 33), ("c", 18), ("d", 41)]
Now, in the sorted list, we know that there will be a contiguous blog of 10 "a"s, followed by a contiguous block of 33 "b"s, and so forth. We can use this information to calculate the offset of each contiguous block up front:
def offsets(keys):
d = {}
offset = 0
for key, occurences in keys:
d[key] = offset
offset += occurences
return d
The key function uses this offset dictionary to look up the current index for any element. Each time we insert an element into position, we increment the relevant offset entry - next time we get to an element of the same type, we will place it in the next position in the contiguous block. We also make a small modification to the algorithm to cater for the progressive position increment process: we start a cycle only when the element is equal to or above the position where it ought to be. Here's a Python implementation:
def offsets(keys):
d = {}
offset = 0
for key, occurences in keys:
d[key] = offset
offset += occurences
return d
def key(o, element):
return o[element]
def cyclesort_general(l, keys):
o = offsets(keys)
for i in range(len(l)):
if i >= key(o, l[i]):
n = i
while 1:
tmp = l[n]
if n != i:
l[n] = last_value
last_value = tmp
n = key(o, last_value)
o[last_value] += 1
if n == i:
l[n] = last_value
break
This algorithm runs in O(n + m), where n is the number of elements and m is the number of distinct element values. In practice m is usually small, so this is often tantamount to being O(n).
The code
As usual, the code for these visualisations have been incorporated into the sortvis project. I've also added the visualisations above to the sortvis.org website.