I like the Hilbert curve. I like sorting algorithm visualisations. I occasionally procrastinate when I should be doing more important things. When all these factors converge, the result is a post like this.

In a previous post, I drew a picture of a Hilbert curve by projecting a Hilbert curve traversal of the RGB colour cube onto a Hilbert curve traversal of the plane (yes, it's a mouthful, but it's a mouthful of awesome). Since then, I've been pondering the general utility of Hilbert curve traversals of the colour cube. In large-scale visualisation, we often want to choose an ordered sequence of colours that have the property that colours close to each other on the sequence are also close to each other visually. The easy way to do this is to restrict yourself to a specific hue, and to vary the intensity. I used this idea in grayscale to generate some previous sorting algorithm visualisations:

Insertion sort

The problem with this approach is that it hugely restricts the number of distinct colours we can use. There are only so many distinct shades of gray the human eye can perceive - I'm already pushing it with 20 distinct colours in the image above. We can do much, much better using the Hilbert curve. Lets assume that human perception of RGB colours is uniform and consistent - that is, that any change along the RGB axes will result in uniformly proportional difference in perceived colour. This assumption is incorrect, but it's good enough as a first approximation. By traversing the RGB colour cube in Hilbert order, we can get a set of colours that are maximally distinct from each other, with near-optimal colour locality preservation (keeping in mind that perfect locality preservation is impossible). In other words, an equidistant sequence of colours that are simultaneously as different from each other as possible, and where colours 'close' to each other on the sequence are as similar as possible. The result is a colour sequence that looks like this:

512-colour Hilbert-order swatch

We do, of course, pay a price for this mathematical marvel: we can't visually compare colours and see their order in the spectrum. When we really want a large ordered sequence of colours, this can be an acceptable tradeoff.

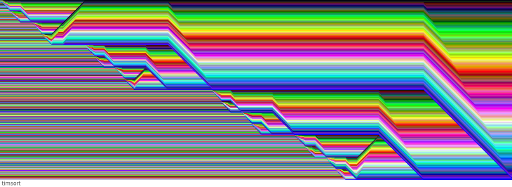
Below is a re-imagining of my previous sorting algorithm visualisations, at a much larger scale than I could achieve using shades of gray. Each image shows a random list of 512 elements being sorted. The images are at a 1-pixel per element resolution, and each element has a distinct colour along the Hilbert RGB cube traversal. The aspect ratios differ, because the width of the images are equal to the number of element swaps that occur during the sorting process. I've left out a number of algorithms that end up being too "wide" to be enjoyable - shellsort and bubblesort, I'm looking at you. Oh, and I make absolutely no claims that these particular visualisations are useful or informative. I made them for the same reason Mallory climbed Everest and the chicken crossed the road: because it's there, and to see what's on the other side. Come to think of it, the Mallory-Chicken Impetus explains rather a lot of what I do.

Selection sort

Selection sort

Insertion sort

Insertion sort

Python's Timsort

I explained the pattern you see below in a previous post visualising Timsort.

Timsort

Quicksort

Quicksort

The code

As usual, I've published the code used to draw the images in this post. I extended scurve, where I'm collecting algorithms and visualisation techniques related to space-filling curves, to draw colour swatches. Then I added added a "fruitsalad" visualisation technique to sortvis, which houses my sorting algorithm visualisation code.